SISTEM KOODINAT POLAR DAN KARTESIUS
Sistem koordinat Kartesius digunakan untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x dan koordinat y dari titik tersebut.
Untuk mendefinisikan koordinat diperlukan dua garis berarah yang tegak lurus satu sama lain (sumbu x dan sumbu y), dan panjang unit, yang dibuat tanda-tanda pada kedua sumbu tersebut
Sistem koordinat Kartesius dapat pula digunakan pada dimensi-dimensi yang lebih tinggi, seperti 3 dimensi, dengan menggunakan tiga sumbu (sumbu x, y, dan z).
Sistem koordinat Kartesius dapat pula digunakan pada dimensi-dimensi yang lebih tinggi, seperti 3 dimensi, dengan menggunakan tiga sumbu (sumbu x, y, dan z).

Gambar 2 - Sistem koordinat Kartesius disertai lingkaran merah yang berjari-jari 2 yang berpusat pada titik asal (0,0). Persamaan lingkaran merah ini adalah x² + y² = 4.
Dengan menggunakan sistem koordinat Kartesius, bentuk-bentuk geometri seperti kurva dapat diekspresikan dengan persamaan aljabar. Sebagai contoh, lingkaran yang berjari-jari 2 dapat diekspresikan dengan persamaan x² + y² = 4.
VEKTOR POSISI
vektor posisi dapat dinyatakan sebagai jumlah vektor dari setiap vektor basis yang sesuai dengan jenis koordinat yang digunakan.
vektor basis adalah vektor yang menjadi vektor dasar/pembentuk/pembangun dari suatu koordinat dan pernyataannya tergentung dari jenis koordinat yang digunakan.
contoh vektor basis:
vektor basis x, y, z dalam koordinat Cartessian
vektor basis r, theta dalam koordinat lingkaran
vektor basis r, theta, pi dalam koordinat Bola
jadi vektor posisi dapat dituliskan sebagai jumlah dari vektor-vektor basis tersebut.
contoh penulisan vektor posisi:
S = 2x +3y + 4z (S, x, y, z adalah vektor)
atau bisa juga hanya ditulis (2,3,4)
bentuk ini memiliki aturan urut yaitu (x,y,z)
setiap masalah dapat diselesaikan dengan sistem koordinat manapun tapi ada beberapa masalah yang dapat dengan mudah diselesaikan dengan menggunakan sistem koordinat yang pas.
sebagai contoh tidak mungkin kita menunjukkan posisi kota jakarta di Bola Dunia (Globe) dengan menggunakan koordinat Cartessian karena vektor posisinya akan sulit dinyatakan. koordinat yang pas untuk masalah tersebut adalah koordinat Bola dengan format (r,theta,pi)
GMB dan GMBB
GERAK MELINGKAR BERATURAN Suatu benda dikatakan bergerak melingkar beraturan (GMB) bila benda
tersebut bergerak dalam lintasan berbentuk lingkaran dan lajunya tetap. Di kehidupan sehari-hari kita akan banyak
menemui kejadian GMB ini. Perputaran jarum jam, revolusi bumi, gerak satelit pada orbitnya, dll. Di sini, harus diingat
bedanya kelajuan dengan kecepatan. (kecepatan merupakan kelajuan yang mempunyai arah). Jadi, meskipun kelajuan
benda pada GMB ini tetap, bukan berarti kecepatannya juga tetap. Kelajuan benda dinyatakan sebagai kecepatan
sudut benda (ω) dikalikan jari-jari (r). v = ω.r Coba perhatikan gambar berikut.
Disana terlihat ada perubahan arah kecepatan (v). Awalnya mendongak ke atas setelah beberapa saat kemudian
menjadi ke arah bawah. Percepatan adalah perubahan kecepatan per satuan waktu, atau : a =
(Δv/Δt)..................................................(1)
akan tetapi, karena kelajuan benda besarnya tetap maka yang berubah adalah arahnya/sudutnya. Dengan menganggap
Δt bernilai kecil, maka Δθ juga bermilai kecil. Sehingga, Δv/v = Δr/r atau bisa kita ubah
menjadi Δv = v.(Δr/r)...............................................(2) Dengan menggabungkan persamaan 1 dan 2 akan kita
peroleh
Jadi, pada GMB kecepatan benda dinyatakan dengan kecepatan sudut dikali jari-jari lingkaran, atau v =
(Δθ/Δt).r = ω.r dan percepatan yang terjadi disebut percepatan sentripetal yang arahnya ke titik
pusat lingkaran yang besarnya :
GERAK MELINGAR BERUBAH BERATURAN Pada GMBB, kecepatan gerak benda selain berubah arahnya juga
berubah besarnya. (Arti kata “berubah beraturan” pada GMBB adalah kelajuan benda berubah secara
teratur). Jadi pada GMBB percepatan terdiri atas 2 macam. Percepatan sentripetal (seperti pada GMB) yang arahnya ke
titik pusat lingkaran, dan percepatan tangensial yang arahnya tegak lurus dengan jari-jari (menyinggung lingkaran). Agar
lebih jelasnya kita nyatakan dalam bentuk vektor.
(menunjukkan searah dengan jari-jari, danmenunjukkan tegak lurus dengan jari-jari)
contoh : Sebuah benda bergerak secara GMBB dengan percepatan anguler sebesar b (rad/s2). maka kecepatannya
sebagai fungsi waktu adalah : v = ω.r =
 ,
, 
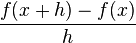 pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut. , seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).
, seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).
